In 2004 Arkowitz and Brown have presented an axiomatization of the
reduced Lefschetz number of self-maps of finite CW-complexes. By a
result of McCord, finite simplicial complexes are closely related to
finite \(T_0\)-spaces. Using this connection, we show that the
reduced Lefschetz number can be generalize to not only self-maps of
finite spaces. Following May, we write \(X^{(n)}\) for the \(n\)th
barycentric subdivision of a finite \(T_0\)-space \(X\). The main
result states that the reduced Lefschetz number is the unique
function \(\lambda\) on the class of maps \(X^{(n)}\to X\) into
integers satysfying the following conditions:
- if \(f\colon X^{(n)}\to X, g\colon X^{(m)}\to X\) are contiguous then
\(\lambda(f)=\lambda(g)\);
- if \(A\subseteq X\) and the following diagram
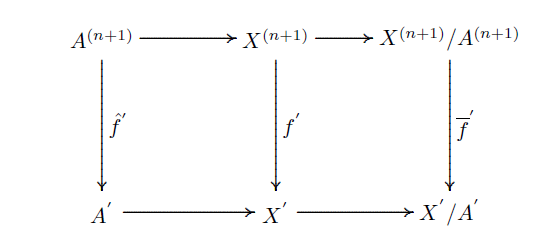is commutative then
\(\lambda(f^{'})=\lambda(\hat{f}^{'})+\lambda(\overline{f}^{'})\);
- for any \(f:X^{(n)}\to Y\) and \(g:Y^{(m)}\to X\) we have
\(\lambda(gf^{(m)})=\lambda(fg^{(n)})\);
- let \(f:\bigvee\limits_{i=1}^n\mathcal{S}^{1,k}\to
\bigvee\limits_{i=1}^n\mathcal{S}^{1,2}\) for \(k\geq 2\),
then \[\lambda(f)=-(\deg f_1+\dots+\deg f_n),\] where
\(f_i=p_ife_i:\mathcal S^{1,k}_i\to\mathcal S^{1,2} \) for
\(i=1,\ldots ,k\) and \(\mathcal S^{1,k}\) are combinatorial
models of the circle \(\mathbb S^1\).
|
